statduck
Variational Inference 본문
목적 VI 그간 추상적으로 알고있었는데, 실제 파라미터 업데이트 및 사용하는 이유 및 맥락을 살펴보기 위함
정의
$$ q = \underset{q \in \mathcal{Q}}{\mathrm{argmin}} \, D_{\mathbb{KL}} \, (q(z) \; || \; p_\theta(z|x)) $$
$$ \begin{align*} \psi^* &= \underset{\psi}{\mathrm{argmin}} \, D_{\mathbb{KL}} \, (q_\psi (z) \; || \; p_\theta (z|x)) \\ &= \underset{\psi}{\mathrm{argmin}} \, \mathbb{E}_{q_\psi (z)} \Big[\log q_\psi (z) - \log \Big( \dfrac{p_\theta(x|z) p_\theta(z)}{p_\theta (x)} \Big) \Big] \\ &= \underset{\psi}{\mathrm{argmin}} \, \underbrace{\mathbb{E}_{q_\psi (z)} [ \log q_\psi (z) - \log p_\theta (x|z) - \log p_\theta (z)]}_{\mathcal{L}(\theta, \psi | x)} + \log p_\theta (x) \end{align*} $$
- known variables $x$
- unknown(latent) variables $z$
- fixed parameter $\theta$
- $p_\theta (z|x)$: original posterior
- $q(z)$: surrogate distribution
기존에는 $q$를 찾는건데, paremetric family $\mathcal{Q}$를 하나 고른다고 가정하고, 해당 패밀리에 속하는 모수 $\psi$ (known as variational parameters)를 찾는 식으로 바꾼다. (분포 가정해야 모수개수가 제한된 곳에서 파라미터 찾을 수 있음)
이 때 위 식에서 loss인 $\mathcal{L}$을 최소화 하는게 목표가 될 것이다. 그리고
$$\mathcal{L}(\theta, \psi | x) = E_{q_\psi (z)} [-\log p_\theta (x,z) + \log q_\psi (z) ] = negative \, \text{ELBO}(L)$$
($L$ for ELBO, $\mathcal{L}$ for loss)
$ D_{KL} \geq 0 $ -> 여기서 ELBO가 expected
결국 다음의 DGM(Directed Graphical Model)을 알고 있다는 가정하에 시작하는데 아래 그래프 구조를 알고있음은 다음 수식을 알고있음과 동일하다. $p(X,Z) = p(X) \times p(Z|X) $

Parameter Estimation: Variational EM
$\theta$를 모르는 경우 MLE로 이를 추정하려고 한다.(하지만 계산 불가능: incompuatble, intractable)
$$ \log p(\mathcal{D}|\theta) = \sum^N_{n=1} \log p(x_n | \theta) L $$
우리가 가정하는 latent variable model에서는 $\theta^{MLE}$를 어떻게 구할까?
$$p(\mathcal{D}, z_{1:N} | \theta) = \Pi^N_{n=1} p(z_n|\theta)p(x_n|z_n,\theta)$$
위 구조에서 local latent variables $z_n$가 hidden이므로 우리가 $p(\theta|\mathcal{D}$를 구할 때는 marginze out(적분으로 해당변수 없애주기) 해주어야 한다. 즉 다음과 같이 local log marginal likelihood를 구해야한다.
$$ \log p(x_n \theta) = \log \Big[ \int p(x_n|z_n,\theta) p(z_n|\theta)dz_n \Big]$$
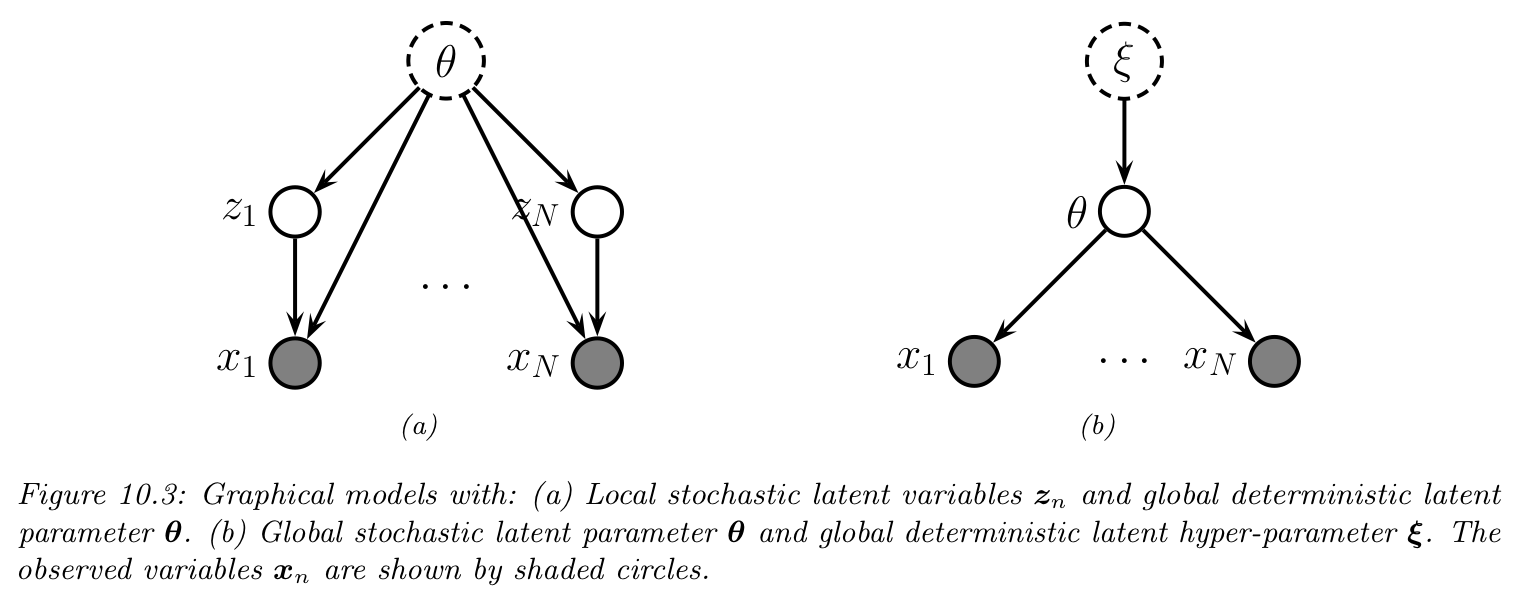
하지만 이 적분계산도 마찬가지로 intractable(상식적으로 $z_1,...,z_n$ 적분 다 해야하는데 계산가능할리가 없음) 하다(Exact posterior normalization과 동일함)
$$ L(\theta, \psi_{1:N} | \mathcal{D}) = \equiv \sum^N_{n=1} L(\theta, \psi_n |x_n) \leq \log p(\mathcal{D}|\theta) $$
그래서 이러한 optimization 문제로 풀어보자는 것이 variational EM algorithm이다.
N개의 latent vector : N개의 prior params $\psi_{1:N}$
- E step maximizing the ELBO wrt ${\psi_n}$ (the variational params)
- M step maximizing the ELBO wrt $\theta$ (model params)
속도 향상을 위해 1)Stochastic VI 2) Amortized VI를 활용할 수 있다.
EM 알고리즘은 실제 Z값을 얻을 수 없는 경우 Z에 대한 기댓값, 즉 $E_z [ln \, p(X,Z |\theta)]$를 이용해 다음을 iterative하게 푸는 것이다. $$E_z [ln \, p(X,Z|\theta)] = \sum_z \underbrace{p(Z| X,\theta)}_{\text{posterior}} \times \underbrace{ln \, p(X,Z|\theta)}_{\text{likelihood}}$$
- E step $Q(\theta, \theta^{old}) = \sum_z p(Z|X,\theta^{old}) ln \, p(X,Z|\theta)$
- M step $\theta^{new} = \underset{\theta}{argmax} Q(\theta, \theta^{old})$
1) Stochastic VI
- 데이터 크기(N)가 큰 경우 학습 속도가 느리다. 따라서 랜덤한 미니배치 $B = | \mathcal{B}|$ 를 데이터에서 뽑는다
$L(\theta, \psi_{1:N} | \mathcal{D} ) = \sum^N_{n=1} L(\theta, \psi_n|x_n) $
2) Amortized VI
https://ricoshin.tistory.com/3
Amortized Inference란?
https://www.quora.com/What-is-amortized-variational-inference What is amortized variational inference? Answer: Let me briefly describe the setting first, as the best way to understand amortized variational inference (in my opinion) is in the context of reg
ricoshin.tistory.com
결국 Inference Network의 파라미터로 학습시킬 파라미터를 바꾼 것이라고 볼 수 있다. $z_n$을 조절하는 파라미터 $\psi_n$을 찾아야하는 문제에서 데이터 $x_n$에서 $z_n$을 추론하는 $\phi$를 찾는 문제로 바뀌었다. 이를 통해 매번 새로운 x가 들어올때(z가 생길 때) 일일이 파라미터를 학습해줄 필요없이 미리 업데이트 한 $\phi$로 추정할 수 있는 장점 획득
$$ q(z_n|\psi_n) = q(z_n|f^{inf}_\pi (x_n)) = q_\phi (z_n|x_n)$$
$$ L(\theta,\phi | \mathcal{D}) = \sum^N_{n=1} [ \mathbb{E}_{q_\phi (z_n | x_n)} [ \log p_\theta (x_n, z_n) - \log q_\phi (z|x_n)]]$$
만약 이를 Stochastic VI와 합치면(미니배치 사이즈 1) 다음과 같다.
$$ L(\theta,\phi | x_n ) \approx N [ \mathbb{E}_{q_{\phi} (z_n|x_n)}[\log p_\theta (x_n, z_n)- \log q_\phi (z|x_n)]]$$
Algorithm 10.1: Amortized stochastic variational EM
- Initialize $\theta, \phi$
- repeat
- Sample $x_n \sim p_\mathcal{D}$
- E step $\phi = argmax_\phi L(\theta, \phi | x_n)$
- M step $\theta = argmax_\theta L(\theta, \phi | x_n)$
- until converged
이 때 M step에서 $\theta$를 업데이트 하는건 gradient update로 가능하지만 E step에서 $\phi$를 업데이트 하는게 문제인데, 위의 로스 $L$에서 이미 $\phi$를 이용하고 있기 때문에 Expectation, gradient 자리 이동이 불가하다.(Gradient-Based VI에서 살펴보자)
Gradient-Based VI
1) choose convenient form of $q_\pi (z)$ 2) optimize the ELBO using gradient based method
$$ \begin{align*} \nabla_\theta L(\theta, \phi | x) &= \nabla_\theta \mathbb{E}_{q_\phi (z|x)} [ \log p_\theta (x,z) - \log q_\phi (z|x)] \\ &= \mathbb{E}_{q_\phi (z|x)} [ \nabla_\theta \{ \log p_\theta (x,z) - \log q_\phi (z|x) \} ] \\ &\approx \nabla_\theta \log p_\theta (x, z^s) \end{align*})$$
where $z^s \sim q_\phi (z|x)$.
$$ \begin{align*} \nabla_\theta L(\theta,\phi |x) &= \nabla_\phi \mathbb{E}_{q_\phi (z|x)} [\log p_\theta (x,z)-\log q_\phi (z|x)] \\ & \neq \mathbb{E}_{q_\phi (z|x)} [ \nabla_\phi \{ \log p_\theta (x,z) - \log q_\phi (z|x) \} ] \end{align*}$$
이 문제를 해결하기 위해 1) reparmetrization trick 혹은 2) blackbox VI 를 이용한다.
Reparameterized VI
목적: latent variable $ z \sim q_\theta (z|X)$ 분포에 대해 gradient 계산을 하기 위해 기존 파라미터에 대해 변수변환을 한다.
변수변환을 통해 궁극적으로 얻고자 하는건 Exchange the position between 'Gradient' and 'Expectation' 이다.
왜냐하면 결국 Expectation이 밖으로 빠져나와야지 몬테카를로 estimation으로 우리가 근사할 수 있기 때문이다.
Change Of Variable 과정($z \rightarrow \epsilon$)
$$ z \sim q_\phi (z|x) \equiv N(\mu, \sigma^2) $$
$$ z \overset{\text{let}}{=} g(\phi, \epsilon) = \mu + \sigma \odot \epsilon \; (s.t. \, \epsilon \sim N(0,1)) $$
$$ p_\epsilon(\epsilon) = f_z (g(\phi,\epsilon)) \cdot \dfrac{\partial z}{\partial \epsilon} = \dfrac{1}{\sqrt{2\pi} \sigma} \cdot exp(-\epsilon^2 /2) \cdot \sigma = \dfrac{1}{\sqrt{2\pi}} \cdot exp(-\epsilon^2/2)$$
So $\epsilon$ does not depend on $\phi$
Finally, This let the exchange the position between $\nabla$ and $\mathbb{E}$ is able.
$$ \nabla \mathbb{E}_{q_\phi (z|x)} [f(z)] = \nabla \mathbb{E}_{p(\epsilon)} [f(z)]$$
This let us propagate graidents back through the $\mathcal{f}$ function.
Gaussian Example (Cov 모양에 따라 3가지 경우로 나뉨) 결론은 reparameterized trick을 적용하기 위해 변수변환을 어떻게 할 것이냐의 문제이다.
Diagonal Covariance
$$ \epsilon \sim N(0,I) $$
$$ z = \mu + \sigma \odot \epsilon$$
Full Covariance
$$ \epsilon \sim N(0,I) $$
$$ z = \mu + L \epsilon $$
$\sum = LL^T$, where $L$ is a lower triangular matrix with non-zero entries on the diagonal.
low-rank plus diagonal Covariance
$$ \sum = BB^T + C^2$$
(Cholesky decomposition)
Automatic differentiation VI
https://arxiv.org/pdf/1603.00788.pdf
- Transform the support of latent variable into real coordinate space
- Compute the ELBO for any model using MC integration
- Stochastic Gradient Ascent to maximize the ELBO and use automatic differentiation
$T \, : \, \Theta \rightarrow \mathbb{R}^D$ : maps from the constrained space $\Theta$ to the unconstrained space $\mathbb{R}^D$
예를 들어 Normal의 분산의 경우에는 0이상이어야하는데, 이러한 파라미터 스페이스를 실수 공간으로 확장시켜주는게 $T$이다.
latent variable에 대해 $u=T(z)$라고 하고 GVI(가우시안 VI)을 적용하면 $q_\psi (u)= \mathcal{N} (u|\mu_d, \Sigma), \; \psi=(\mu,\Sigma)$
변수변환에 의해 다음과 같이 바뀐다.
$$ p(u) = p(T^{-1}(u))| \, det(J_{T^{-1}}(u))|$$
이제부터 variational parameter는 $u$이다. 그래서 ELBO도 $u$에 대해 정의가 되어야 한다.
$$ \begin{align*}L(\psi) = \mathbb{E}_{u \sim q_\psi (u)} [ \log p(D|T^{-1}(u)) + \log p(T^{-1}(u)) + log | \, det(J_{T^{-1}} (u)) | ] + \mathbb{H}(\psi) \end{align*}$$
Blackbox Variational Inference
$$ \tilde{L}(\psi, z) = log p(z,x) - log q_\psi (z) $$
$$ L(\theta) = \mathbb{E}_{q_\theta (z)} [ \tilde{L} (\theta,z)]$$
Coordinate ascent VI
$$ q_\psi (z) = \Pi^J_{j=1} q_j(z_j)$$
This is called the mean field approximation
'Machine Learning' 카테고리의 다른 글
| ML Study(1) - Kernel, Variational Inference, Tree methods (0) | 2023.08.07 |
|---|---|
| (ENCO)Efficient Neural Causal Discovery Without Acyclicity Constraints - review (0) | 2023.07.14 |
| Bi-Tempered Logistic Loss (0) | 2023.04.11 |
| ChatGPT는 수능 수학을 풀 수 있을까?(오기편) (0) | 2023.02.12 |
| ChatGPT는 수능 수학을 풀 수 있을까? (0) | 2023.02.12 |




