statduck
Bi-Tempered Logistic Loss 본문
이진분류 문제에서 로지스틱 모형으로 문제 해결함에 있어 Bi-Tempered Loss를 이용할 수 있다.
loss function가 convex인 경우에 decision boundary에서 멀리 떨어진 mislabeled point가 모형에 악영향을 미친다.
근거논문: https://link.springer.com/article/10.1007/s10994-009-5165-z
그러므로 convex형태인 cross entropy를 tempered version으로 치환해서 문제를 해결하자.
mislabled point는 Deicison Boundary와의 거리에 따라 다음 두 개의 케이스로 나뉘고 각 케이스를 해결하기 위해 손실 함수와 추정 함수를 각각 temper시킨다.
Case1) Mislabeld Point far from Deicison Boundary
cross entropy: $L(y,\hat{y}) =\sum_c y_c log \hat{y}_c$
temepred version: $L(y,\hat{y})=\sum_c \Big[ y_c(log_{t_1} y_c - log_{t_1}\hat{y}_c)-\dfrac{1}{2-t_1}(y_c^{2-t_1}-\hat{y}_c^{2-t_1})\Big] $
이 때 $log_t (x) = \dfrac{1}{1-t}(x^{1-t} - 1) $이다.
Case2) Mislabled Point near Deicison Boundary
Standard Softmax: $\hat{y}_c = \dfrac{a_c}{\sum^C_{c'=1} exp(a_c')}=exp\Big[ a_c - log \sum^C_{c'=1} exp(a_c') \Big]$
Tempered Softmax: $\hat{y}_c = exp_{t_2} (a_c -\lambda_{t_2}(a)) s.t. \sum^C_{c=1}exp_{t_2}(a_c-\lambda(a))=1$
이 때 , a는 logit vector이며 exp_t(x) = [1+(1-t)x]^{1/(1-t)}_+이다.
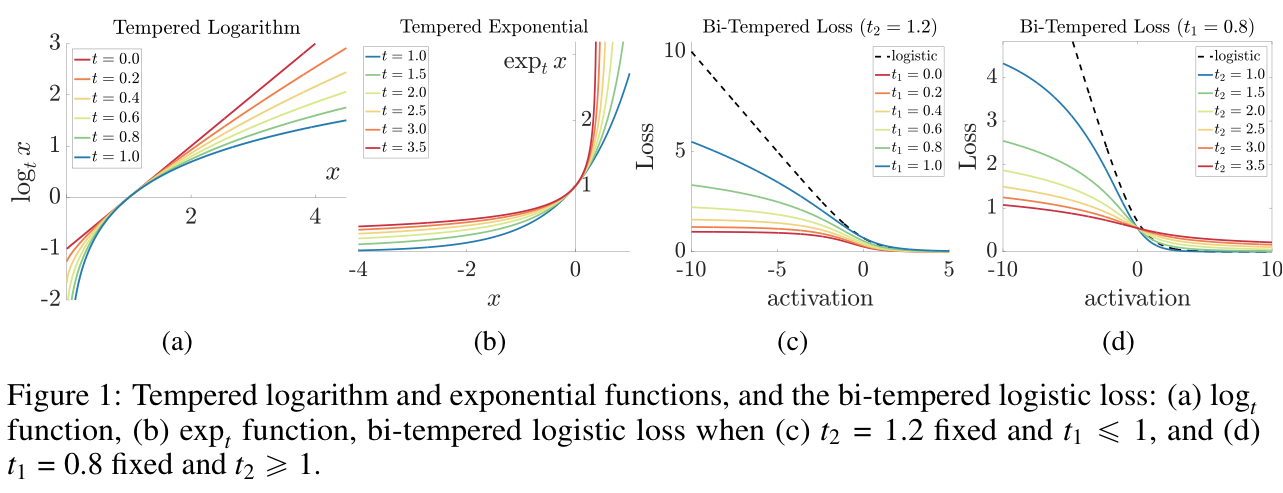
결국 Tempered 된다라는 말은 기존의 성질을 죽여주는 것을 의미하고, 기존 함수 꼴에서 아웃라이어에 취약했던 특성을 약화시켜주는걸로 이해할 수 있다. Case1)에선 손실함수가 경계(bound)를 가지는 식으로 변화되었다. 손실 함수를 최소화시키는 파라미터를 찾는 과정에서, 손실 함수가 특정 값을 넘지 않도록 설정하는 것이다. 학습되는 파라미터를 변경할 때마다 Deicison Boundary 모양이 바뀔텐데 모양이 바뀌어서 아웃라이어 분류를 잘하던지 못하던지 간에 크게 영향을 안받도록 조절해준다. Case2)에선 추정함수가 heavy tail이 되도록 모양을 바꿔준다. heavy tail로 바꿔주면 무엇이 좋냐면,
Effect
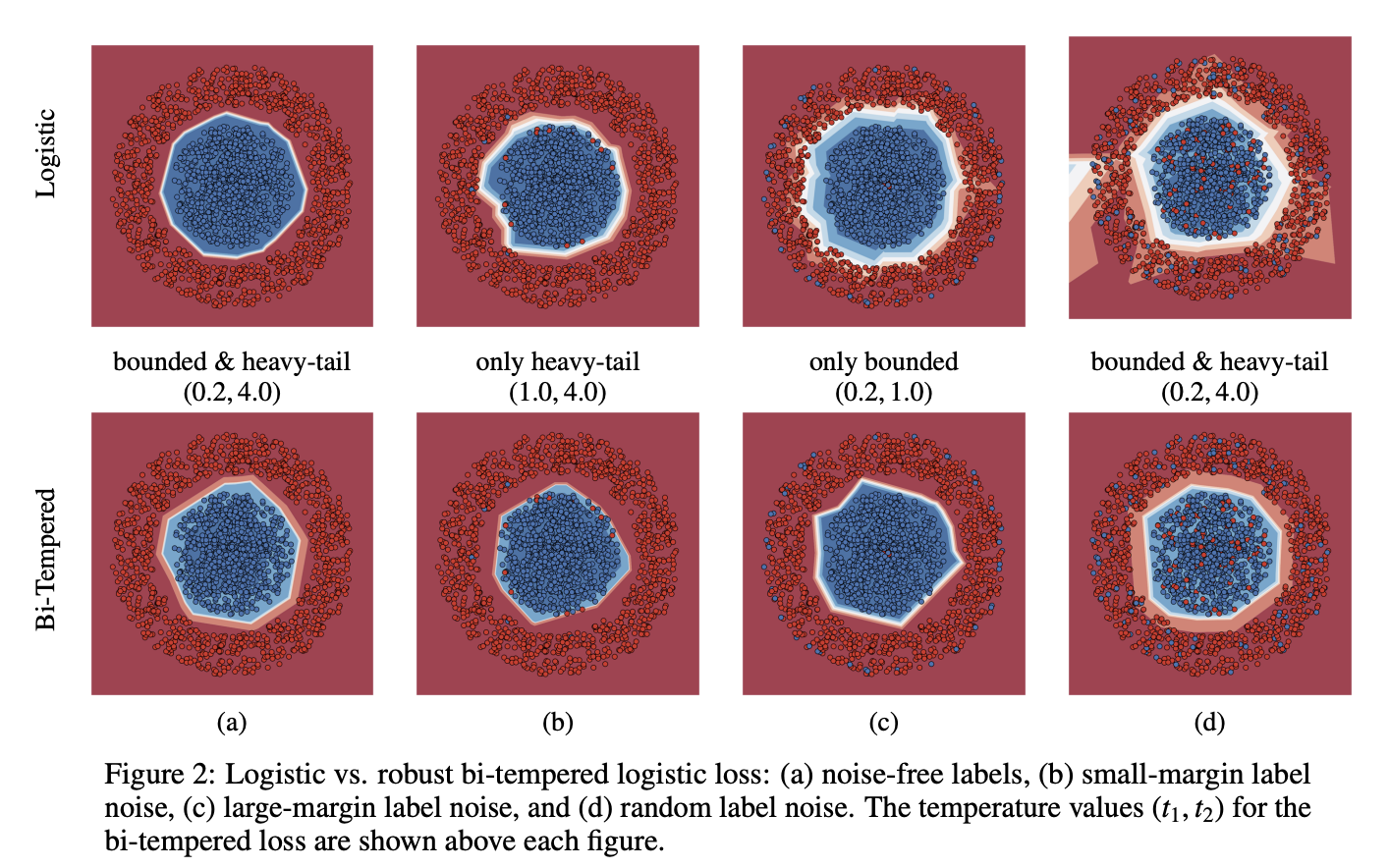
아래 ref 에서 얻어온 결과인데
(b)는 Case2)에 해당하고 (c)는 Case1)에 해당한다. 각각에 대해 일반적인 로지스틱 모형의 경우에는 mislabled point를 좇아 경계선이 더 넓어지는 걸 확인할 수 있지만 bi-tempered loss의 경우에는 강건한 구분선을 유지할 수 있음이 확인가능하다.
(이 때 $ 0 \leq t_1 < 1, t_2 >1$ 조건을 만족해야 각각 bounded loss function, tempered softmax with heavy tail이 되어 효과가 있다.)
실제 뉴럴넷 레이어에서 어떻게 적용되는지는 아래 레퍼런스를 참조하자.
'Machine Learning' 카테고리의 다른 글
| ML Study(1) - Kernel, Variational Inference, Tree methods (0) | 2023.08.07 |
|---|---|
| (ENCO)Efficient Neural Causal Discovery Without Acyclicity Constraints - review (0) | 2023.07.14 |
| ChatGPT는 수능 수학을 풀 수 있을까?(오기편) (0) | 2023.02.12 |
| ChatGPT는 수능 수학을 풀 수 있을까? (0) | 2023.02.12 |
| GAN (0) | 2023.01.06 |




