statduck
[ESL CH2] Overview: Supervised Learning 본문
Two Simple Approaches to Prediction: Least Squares and Nearest Neighbors.
When input vectors are given, how do we predict the output vector? There are many modeling methods available and the choice of methods depends on the nature of the problem and data
Linear Models and Least Squares
Linear regression has been a commonly used method to solve problems where we need to predict a continuous output variable based on one or more input variables.
$$ \hat{Y} = \hat{\beta}_{0}+\Sigma^{p}_j{X_j \hat{\beta}_j} $$
$\hat{\beta}_0$ represents the intercept or bias term, while the other $\hat{\beta}_j$'s represent the coefficients for input variables. These coefficients indicate the power of each input variable in predicting the output. The above expression satisfies the linear relationship, so we call it linear model.
Our goal is to predict function in a p dimensional input space.
$$ \hat{Y} = X^T \beta=f(X) $$
Which method would be best to find f(function)? The function should satisfy linearity and the support of this function must be on a p dimension. The function should reflect the shape of our data with these basic assumptions. We already checked the form is linear so we just need to know the parameter beta.
Parameter is thing we want know, but we don't know. Parameter reflects the information of population. Normally to inference parameter we make use of statistic(통계량) which is the function of some variables following some probability distribution.
The beta above expression is not the value from random sample. To estimate the parameter beta, we just handle with optimization problem: mimizing the error.
Find the beta that minizes the error!
Least Square method
Let's define the error. There are several definitions of error and we use L2 norm(Squared norm) in this post.(L1 norm(absolute norm) coule be used, but it becomes hard to find the beta minimizng error.)
$$
RSS(\beta)=\Sigma^{N}_{i=1}{(y_i-x_i^T\beta )^2}
$$
Residual sum of squares(RSS) is a quadratic form of beta. This form always have minimum value, so all we have to do is just find the value makes derivative form be equal to zero.
$$
RSS(\beta) = (\mathbf{y}-\mathbf{X}\beta)^T(\mathbf{y}-\mathbf{X}\beta) \
\mathbf{X}^T(\mathbf{y}-\mathbf{X}\beta)=0 \
\hat{\beta}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}
$$
If $X^TX$is nonsingular, beta has a unique solution.
Classification Situation
When it comes to linear model, we usually regard the target variable continuous. We call this situation prediction case. However, there is a case where the target variable is discrete. The variable would have just zero or one.(For example, whether a company would bankrupt or not.) In specific, let's assume the target have [0,1]. We can derive an estimated beta value, and predicted y hat through RSS method. This y hat is still a continuous variable so This variable has to be transformed into discrete variable(Threshold(cut-off) setting is needed.)
$\hat{g}=I{(\hat{y}>0.5)}$ only have value zero or one.
$$
\hat{y}=X^T\beta \
\hat{g}=I(\hat{y}>0.5)=I(X^T\beta>0.5)
$$
${x|x^T\hat{\beta}=0.5}$is called a decision boundary. $X^T\beta$ means an inner product of two vectors. Input space is $\mathbb{R}^2$, so this inner product means a line.
We have to check Our decision boundary is good for classfication.
For checking, we should measure the ratio of correct and wrong classification. When there are a lot of wrong-classified values, we need to figure out the reason. It would be because of wrong model or just due to an inevitable error.

Inevitable error varies with the background of data. Let's assume two scenarios.
Scenario 1 : The training data in each class were generated from bivariate Gaussian distributions with uncorrelated components and different means. (A linear decision boundary is good.)
Scenario 2 : The training data in each class came from a mixture of 10 low variance Gaussian distributions, with individual means themselves distributed as Gaussian. (Clustered Gaussian -> nonlinear and disjoint decision boundary is good.)
First one is the situation where data from two groups are not related each other. In the second one, data from two groups are related each other(linear model is not good.)
Nearest-Neighbor Methods

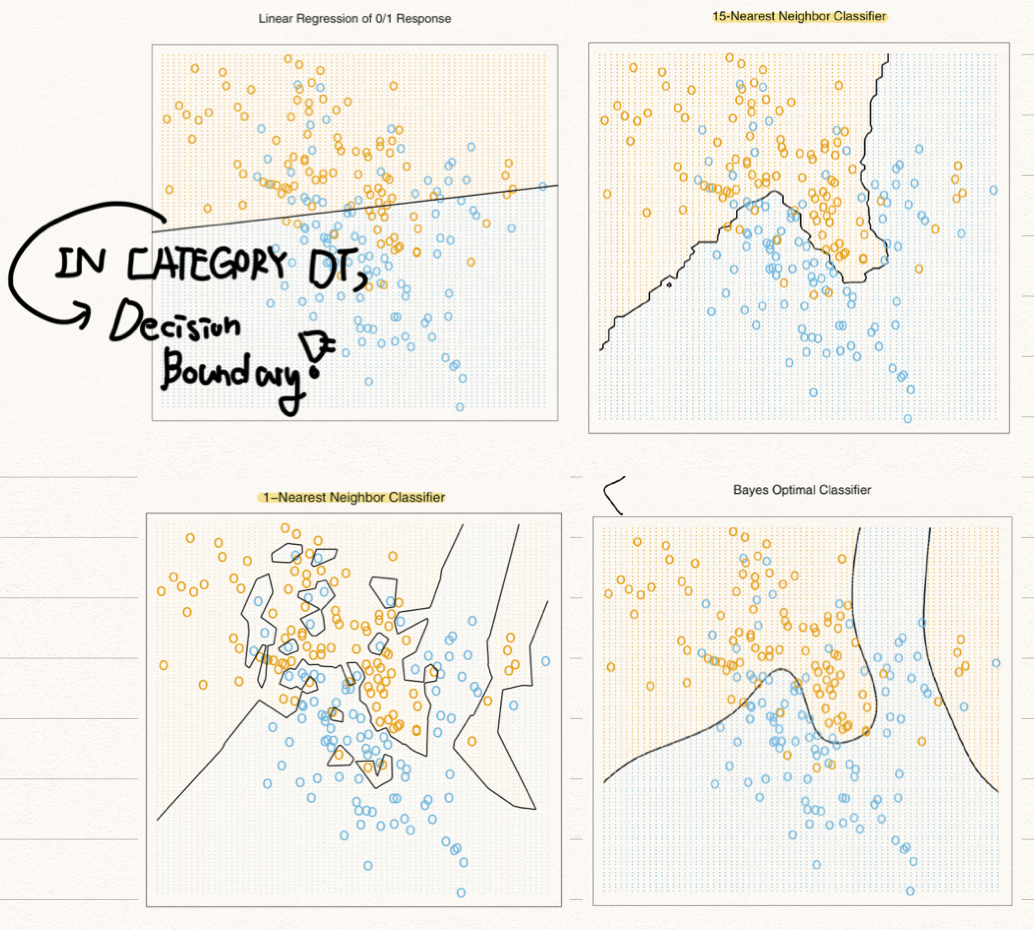
In a classification situation, there is a method called the Nearest-Neighbor Method, which is an alternative to Least Squares Method. Least Squares Method finds the extreme point in a function to minimize the error, while Nearest-Neighbor is the way to estimate a value using the average of nearby values.
Linear Regression 0/1 Response
$$
\hat{Y}(x)=\frac{1}{k}\Sigma_{x_i\in N_k(x)}{y_i}
$$
In the Nearest-Neighbor methods, we need to define a training set $\mathcal{T}$. For example, if we are h is a set of train data set that contains like (0,1), (1,2). The dimension of $\mathcal{T}$is the sum of input and output dimension.
$N_k(x)$is Neighborhood of x defined by the k closest points $x_i$. When we define the concept of open and closed we need to deal with the definition of Neighborhood. Let's think about a circle in two dimension: Open ball
$$
N_r(x)={y\in X:d(x,y)<r}.
$$
K-Nearest Neighbor Classifier
We do a major voting. If over 50% nearby train data is blue, we want to say a test data is blue.
From Least Squares to Nearest Neighbors
Scenario 1 : Linear model is good to fit. We sample from each classes that follow Bivariate Gaussian distributions.
Scenario 2 : Nearest Neighbors is good to feat. From$N((1,0)^T, I)$ we generate $b_k$ and from $N((0,1)^T, I)$ we generate $r_k$(k is the integer from 1 to 10) Here is an example of blue class.
First, we choose the average value randomly and generate $N(b_k,I/5)$. We take some values from this distribution. In this way, we generate one hundred data from each classes(blue and red classes). Total two hundred data are generated, and this data is mixture gaussian cluster in each classes.
Variation of Least squares&KNN is solving so many problems.
A variation of Least Square
Local regression - Fitting a model only using the nearby data.(It is the combination of Least Square and NN) We have to decide the width that determine how many data would be included.
Linear model with a basis expansion - Make a variation of data matrix and make a complicated model.
A variation of KNN.
Kernel method - In KNN, we put a discrete weight(0,1) on data but in kernel method we use a continuous weight from 0 to 1.
'Machine Learning' 카테고리의 다른 글
| Orthogonalization (0) | 2022.05.27 |
|---|---|
| Linear Method (0) | 2022.05.27 |
| Statistical Decision Theory (0) | 2022.05.27 |
| Weighting procedure (0) | 2022.05.27 |
| Curse of dimensionality (0) | 2022.05.26 |

